2025 Devlog

Also available as RSS. See archive for past years.

🕓 A More Objective Approach to Optimization

2025-04-22

A couple of weeks ago while working on the beta release of my ECS, I noticed my command buffer abstraction was slow.

It turns out I was assuming the optimizer could do a few things it couldn’t. The fix wasn’t all that interesting, but it’s worth considering–how do you catch this sort of mistake?

For hot paths you could could manually check the generated code, but if you’re trying to analyze your entire program you’re going to want a profiler.

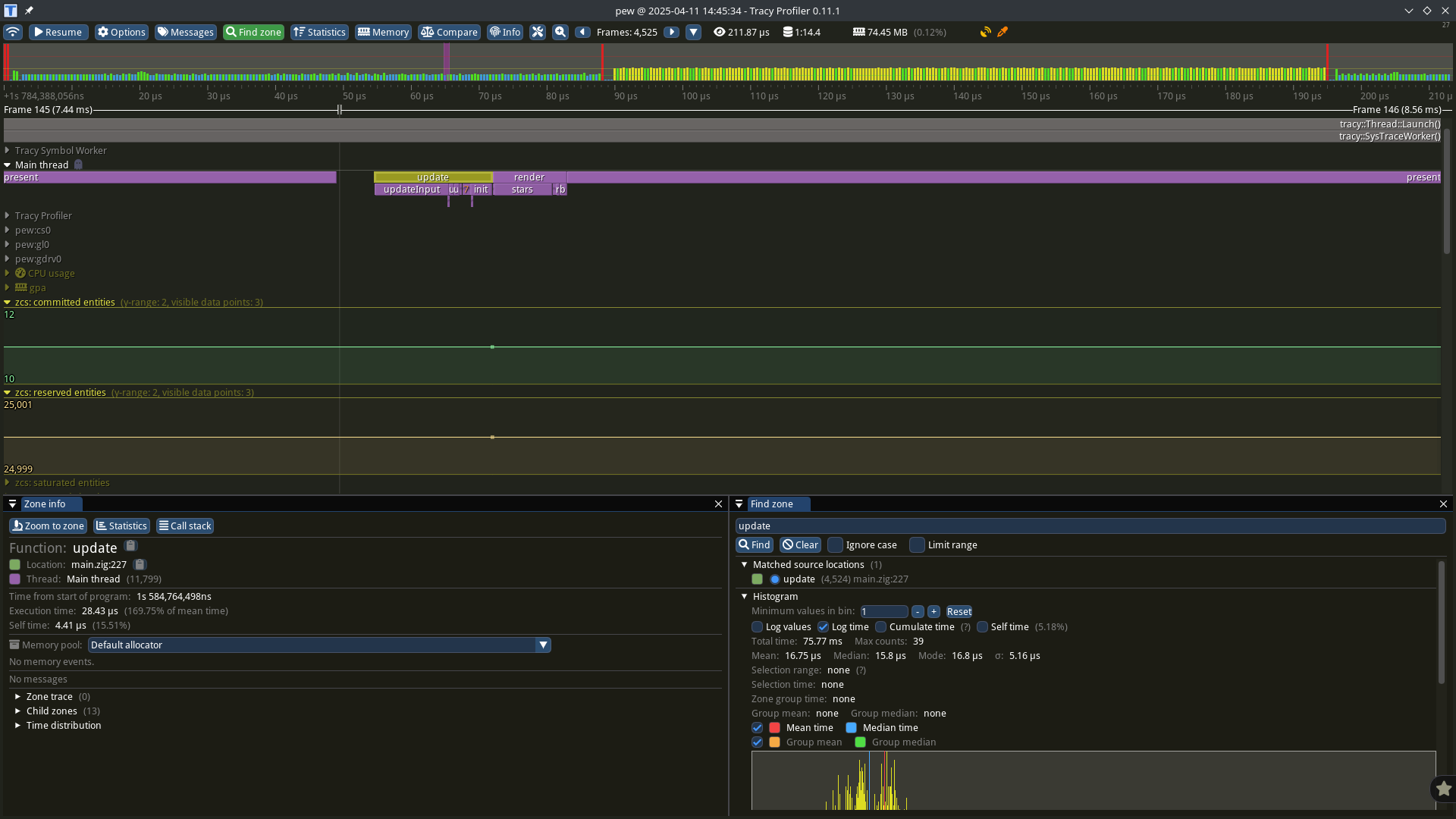
screenshot of the Tracy profiler
I use Tracy, here are my Zig bindings.

Alright, you’ve installed a profiler and instrumented your code–what next? It’s showing you a bunch of numbers, how do you assign meaning to them?

What counts as slow?

A reasonable but boring answer is that it’s context dependent. If you’re making a video game you might measure how many milliseconds the operation takes on your min spec hardware, and then compare that to your frame budget.

This is pragmatic, but it’s also subjective–how do you set the frame budget? How much time should you budget for physics? For rendering? How much headroom should you leave for the inevitable future gameplay features you haven’t thought of yet?

the fastforward feature in Way of Rhea
Fast forward was added to Way of Rhea late in development and required running multiple full-frame updates per frame–good thing I left enough headroom!

Answering the subjective question is it fast enough is part of the art of game development. However, there’s a more objective followup you should also be asking: How fast is it possible to go?

In theory this could be a very tough question to answer, but in practice it’s usually not. Here’s the answer for filling a command buffer:

@memcpy(cmdbuf, cmds);

You’re not gonna beat that. But you should probably try to tie it.

Comparisons to memcpy, ArrayList, and MultiArrayList are often very useful, because a lot of seemingly complex operations boil down to filling a buffer or buffers with data, and maybe doing some mild processing along the way.

If you can’t imagine how your operation could be thought of in these terms, you might want to double check that you really understand the work that’s being done.

Filling a command buffer is ultimately just copying bytes into an array, so we can determine our baseline by just copying the bytes of an example command buffer from one place to another. If we want to be slightly more fair, we can append the commands one at a time to an array list.

If you’re already tied with the baseline, great. Your work here is done.

What if it’s taking longer?

A character from Way of Rhea saying

If the cause isn’t obvious, you can iteratively modify a copy of your algorithm–at the expense of correct results if needed–until the code is identical to the baseline.

At some point, one of these modifications is guaranteed to cause your operation to exhibit comparable performance to your baseline.

Congratulations, now you know both objectively how fast it’s possible to go, and what’s holding you back from achieving that performance!

Once you’ve maxed out this test it’s worth considering whether it’s possible to reasonably encode the same data in less bytes, but that’s a whole separate topic…

🧾 Fast Quaternion Normalization Proof

2025-03-02

In my last post, I advocated for two different methods of accelerating inverse square roots when normalizing of quaternions:

  1. An approach for values very near to 1
  2. An approach for all other values

I was able to show empirically that method 1 converges for a reasonable range of inputs, but wasn’t able to prove it.

Matthew Lugg just sent me a proof that it converges for values between 0 and ~1.56!

In practice I switch to method 2 if I expect to need more than one iteration. Having a proof for the range of values it eventually converges for potentially allows for more precise trade offs, and at the very least gives me peace of mind that it’s correct within the range I’m using it.

My description of their proof follows.

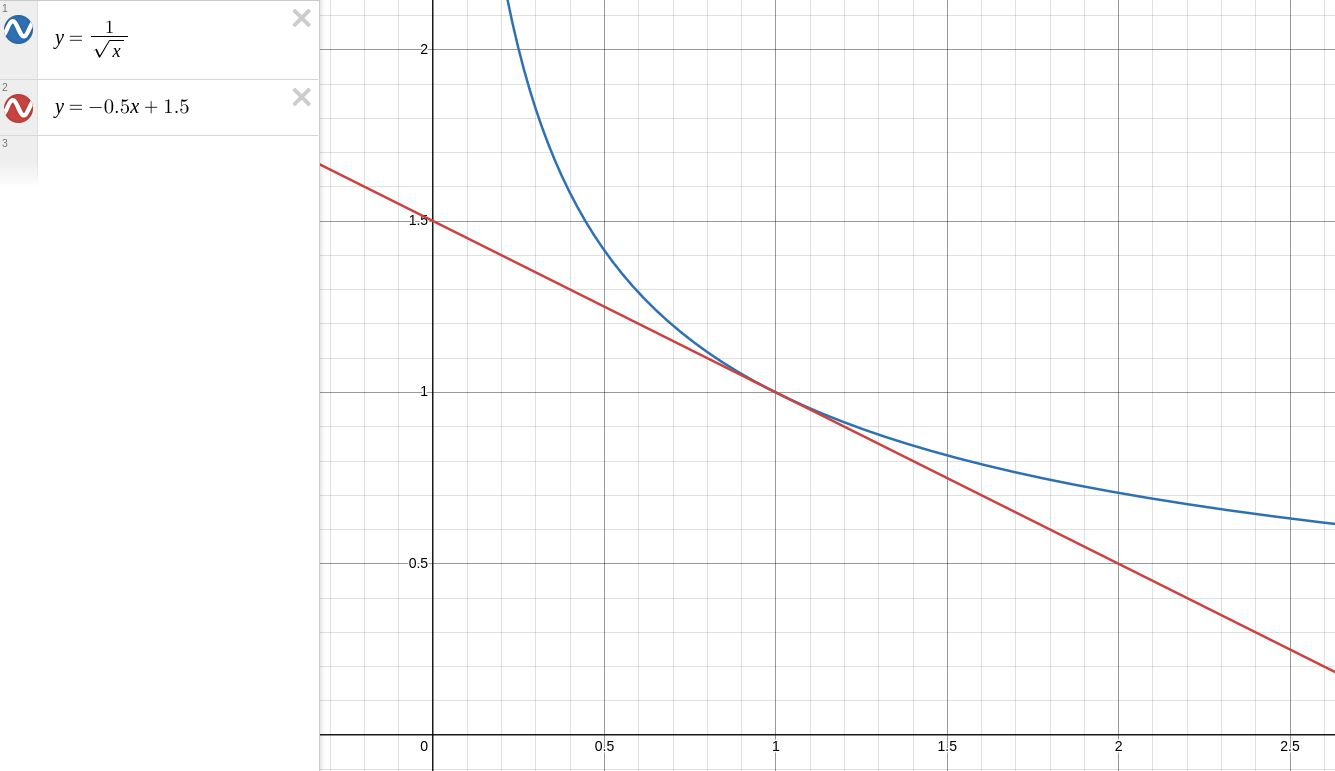
Consider the approximation:

1/sqrt(x) ~= -0.5x + 1.5

Using this to normalize a quaternion, you get:

q / sqrt(magSq(q))

If we substitute in our inverse square root approximation, we end up with the following equation:

q * (-0.5 * magSq(q) + 1.5)

Since all we’re interested in here is the magnitude, let’s rewrite this in terms of the magnitude. Take x to be the original magnitude, and y to be the approximately normalized magnitude:

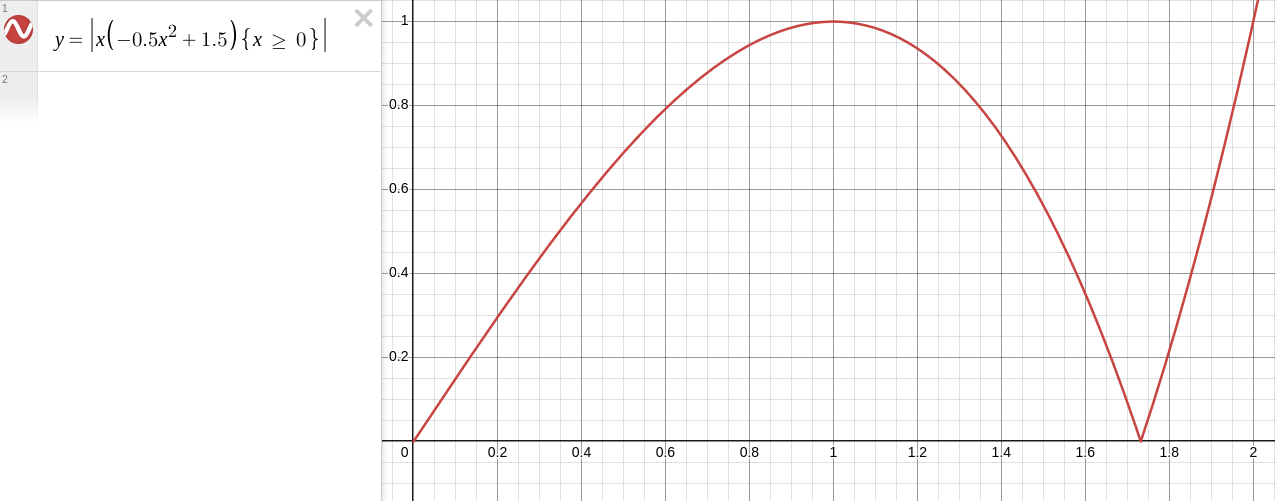
y = |x * (-0.5x^2 + 1.5)|

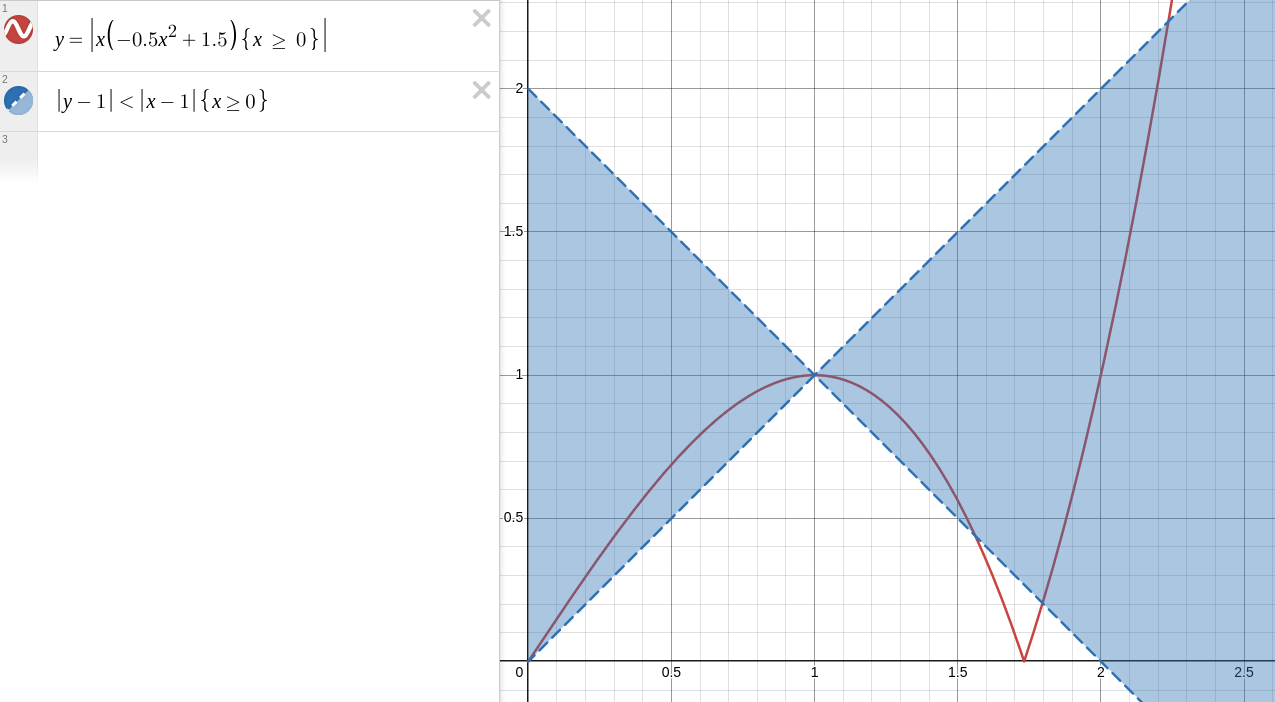
If we can show that within a given range out result y is always closer to 1 than our input x, then values in that range must converge.

We can do this by overlaying |y - 1| < |x - 1| on our graph. Anywhere this intersects with out curve, the approximation must converge:

This is actually overly conservative, technically we could bounce further away before eventually converging–we’ll come back to this idea later.

The red line first crosses the blue area at 0, and then again at near 1.55. Let’s calculate the exact intersection:

# System of equations
y = 2 - x
y = |x * (-0.5x^2 + 1.5)|

# Substitute and simplify so we can solve for 0s
2 - x = |x * (-0.5x^2 + 1.5)|
0 = |x * (-0.5x^2 + 1.5)| - 2 + x
0 = |-0.5x * x^3 + 1.5x| - 2 + x

# Flatten the absolute value, discarding the second intersection
0 = -0.5x^3 + 2.5x - 2

Now we have a cubic equation. We can solve this ourselves, or throw it into a tool like Wolfram Alpha to get the intersection:

x = 0.5 * (sqrt(17) - 1) = 1.5615528128088303

So, our approximation must converge in the range (0, 1.5615528128088303)!

We could stop here, but my original claim was that this would converge until around ~2.24, which includes that suspicious area of the graph where the red line temporarily stops intersecting the blue area:

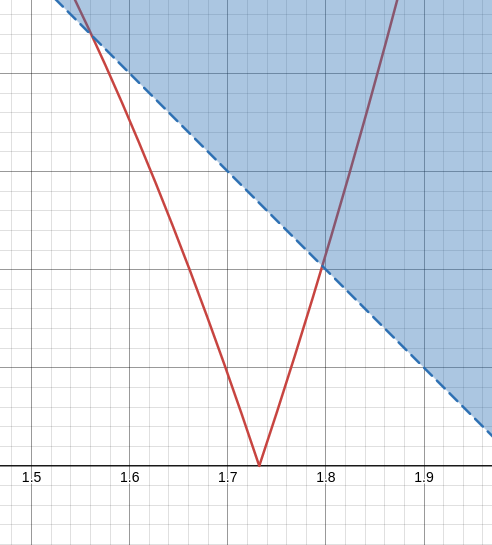
Remember when I said that checking for intersection with the blue area was overly conservative? It’s possible to get further from normal before eventually converging.

If you consider that all of the points in the problem area have y values of values between 0 and 1, it’s clear that any magnitudes in the problem area immediately yeet themselves out of the problem area into the left side of the plot, and therefore aren’t an issue.

…except the point that bounces off the x axis. At zero, our approximation outputs zero and gets stuck. So for this single point at exactly sqrt(3), it will fail to converge.

Do any other points eventually send us to sqrt(3)? If so, they’ll also diverge.

We don’t have to worry about points in the area we already proved converges since they always get closer to 1 and would have to get further from 1 to reach sqrt(3). However, this problem area might have more divergent points!

If we solve for where our approximation outputs sqrt(3), we get another divergent input. We can repeat this process iteratively to generate more divergent inputs:

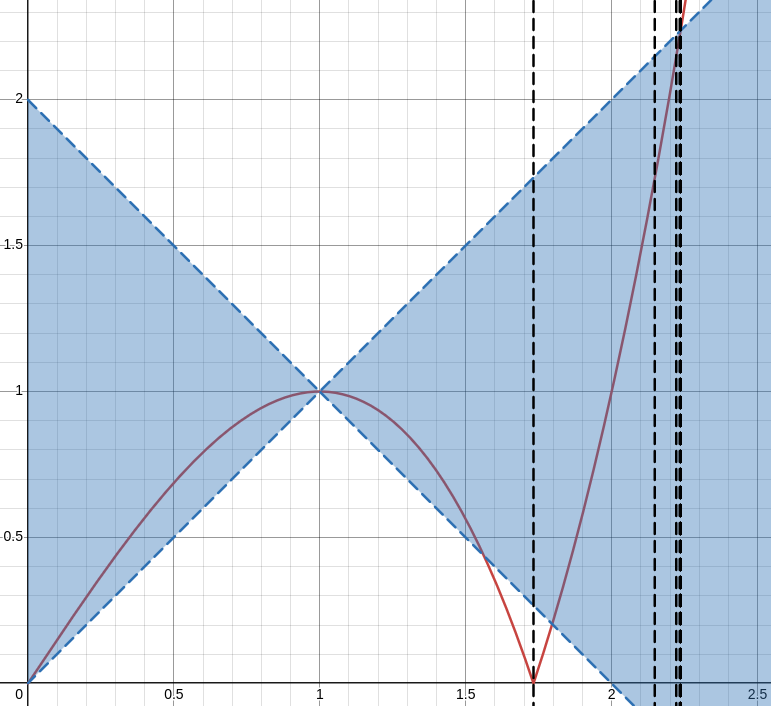
There appear to be an infinite number of these divergent inputs approaching sqrt(5). I was never going to catch this empirically, which is why it’s good to have proofs of this stuff.

It’s probably not possible to represent any of these precisely enough with 32 bit floats to trigger the issue, but now we have peace of mind that non shenanigans like this are waiting for us as long as we stay in that lower range.

In conclusion, the proposed approximation is proven valid for all magnitudes in the range (0, 1.5615528128088303), or more precisely, (0, 0.5 * (sqrt(17) - 1)), which is more than large enough for our purposes.

Outside of this range, you’ll start to have problems.

Thanks again to Matthew Lugg for figuring out this out and letting me share!

🔄 Fast Quaternion Normalization

2025-02-27

Floating point division is slow, and square root is slower. What if I told you that you could approximate 1/sqrt(x) as y = -0.5x + 1.5?

Looks pretty bad right? Try zooming in.

Hmm. Not so bad when you’re near x = 1.

If you’re using 1/sqrt(x) to normalize a quaternion after multiplication, this is likely all you need.

Multiplying two normalized quaternions by each other produces a third normalized quaternion with only a tiny bit of rounding error, so you’re always dealing with magnitudes near one. You just need to keep it from drifting so that your eventual rotation matrix doesn’t inadvertently scale your object.

This function isn’t magic–it’s just the tangent line of y = 1/sqrt(x) at x = 1. You can evaluate it in one instruction if your target supports fused multiply add:

/// Very fast approximate inverse square root that only produces usable
/// results when `f` is near 1.
pub fn invSqrtNearOne(f: anytype) @TypeOf(f) {
    return @mulAdd(@TypeOf(f), f, -0.5, 1.5);
}

(Side note–if this approximation is applied iteratively, the quaternion will approach normalcy if its initial magnitude is in the range (0, ~2.24), outside of that range it diverges. I verified this empirically but I’m not a good enough mathematician to prove it. If you manage to prove it let me know! Proof with corrected range is here!)

Alright, but what if you’re not near one? Maybe you lerped two quaternions together, or need a fast approximate inverse square root for some other purpose.

Turns out most CPUs have a hardware instruction for this now (e.g. on x86 it’s rsqrtss.) I’m not aware of any languages with platform independent intrinsics for this operation, but here’s a quick Zig snippet that will generate the instruction if your target supports it:

/// Fast approximate inverse square root using a dedicated hardware
/// instruction when available.
pub fn invSqrt(f: anytype) @TypeOf(f) {
    // If we're positive infinity, just return infinity
    if (std.math.isPositiveInf(f)) return f;

    // If we're NaN or negative infinity, return NaN
    if (std.math.isNan(f) or
        std.math.isNegativeInf(f) or
        f == 0.0)
    {
        return std.math.nan(f32);
    }

    // Now that we've ruled out values that would cause issues in
    // optimized float mode, enable it and calculate the inverse square
    // root. This generates a hardware instruction approximating the
    // inverse square root on platforms that have one, and is therefore
    // significantly faster.
    {
        @setFloatMode(.optimized);
        return 1.0 / @sqrt(f);
    }
}

This may also generate some extra instructions to refine the approximation. You could sidestep this if it’s undesired by writing per platform inline assembly, but it’s very fast regardless.

The above snippets are from my work in progress Zig geometry library for gamedev.

🧮 Fused Multiply Add

2025-02-22

Quick performance tip. If you’re comfortable requiring support for FMA3 you should probably be using your language’s fused multiply add intrinsic where relevant.

For example, in Zig you’d replace a * b + c with @mulAdd(f32, a, b, c). This is much faster, and more precise.

This is an easy optimization, but the compiler can’t do it for you because replacing your arithmetic with more precise arithmetic isn’t standards compliant.

(Unless you’re using –ffast-math, then all bets are off WRT precision and you can just let the compiler do its thing.)

The only catch is, make sure you’re actually setting your target correctly! The compiler can’t ignore your request for muladd since that would change the precision of you result, so if you’re targeting a baseline CPU that doesn’t have it, you’ll end up emulating it in software and you’ll go slower instead of faster.

On desktop “big” core Intel & AMD CPUs have FMA since 2015, “small” core CPUs got it more recently.

Join my newsletter

Receive an email when I publish writing on game development.

You can unsubscribe at anytime.